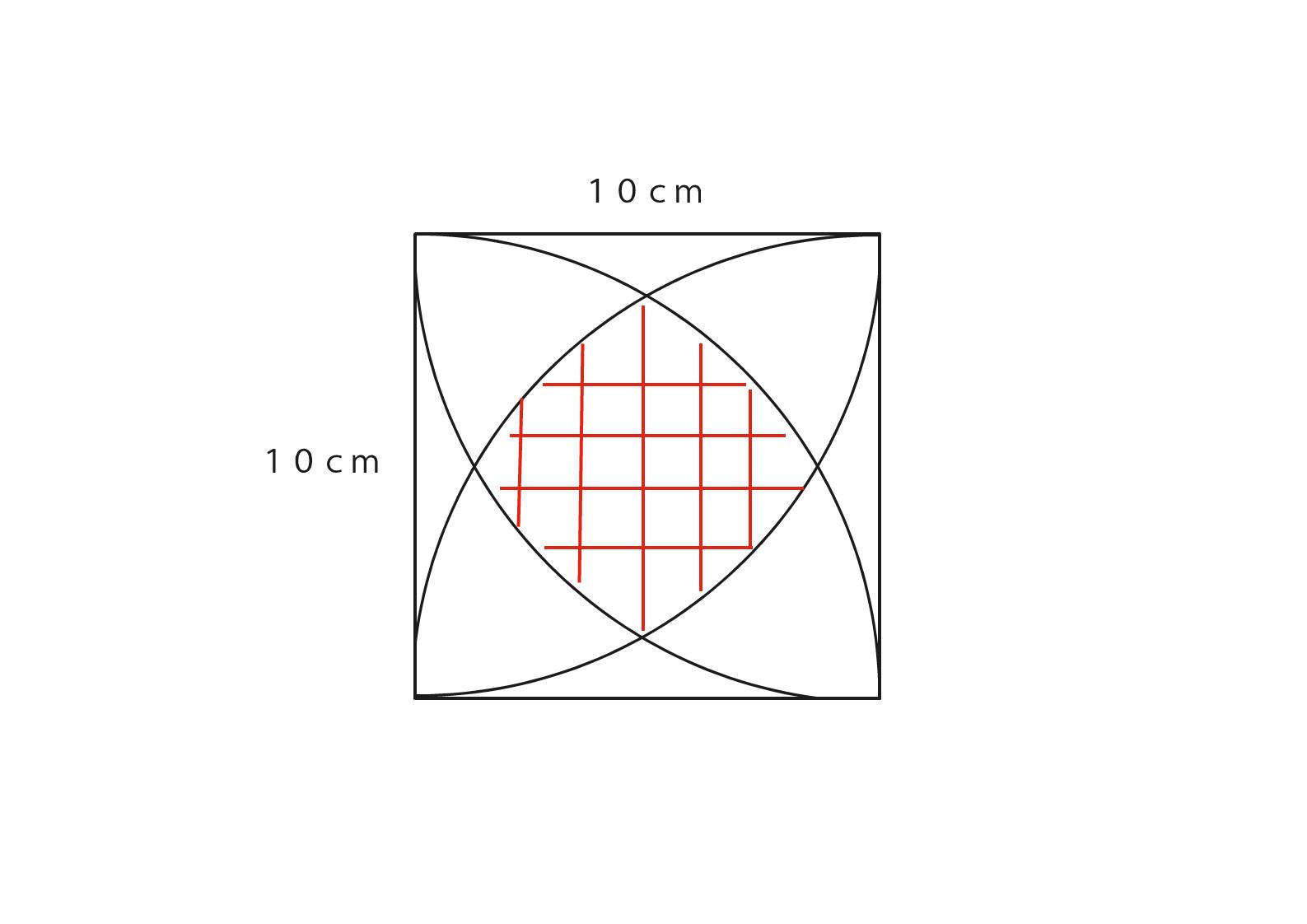
ちょっと難しい図形問題です。
解説は下にあります。
解説
まずは下の図のように正方形から緑色の図形を4つ引くことで真ん中の赤色の面積をもとめます。
緑色の図形の面積は図のように補助線を引いておうぎ形をつくりそこから余分な部分の面積を引いてもとめます。

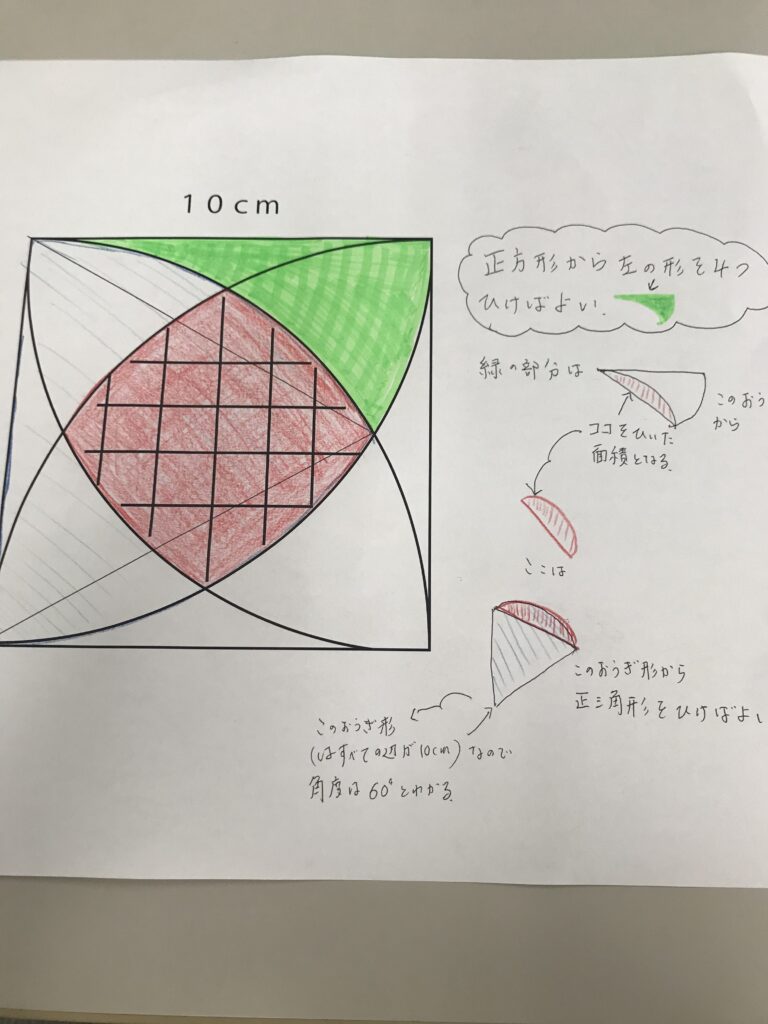
図のように補助線を引くと緑のおうぎ形の中心角は30°であるとわかります。
よってこのおうぎ形の面積は10×10×π×30/360となり
50π/6 となります。
次にもう1つのおうぎ形の面積を求めます。
このおうぎ形は中心角が60°なので10×10×π×60/360となり
50π/3 となります。
先ほどもとめたおうぎ形から以下の正三角形の面積を引くと赤い部分の面積がでます。
この正三角形の面積は三平方の定理で高さを求めて25√3となります。
よって赤い部分の面積は50π/3−25√3 となります。
よって下の緑の部分の面積は最初に求めたおうぎ形から赤い部分を引けばよいので
25√3−50π/6 となります。これが4つあるので×4をして
100√3−100π/3となります。
これを大きな正方形から引けばよいので