正多面体についてまとめてみました。
中学数学・高校数学ともに出てきますのでしっかり理解しておきましょう。
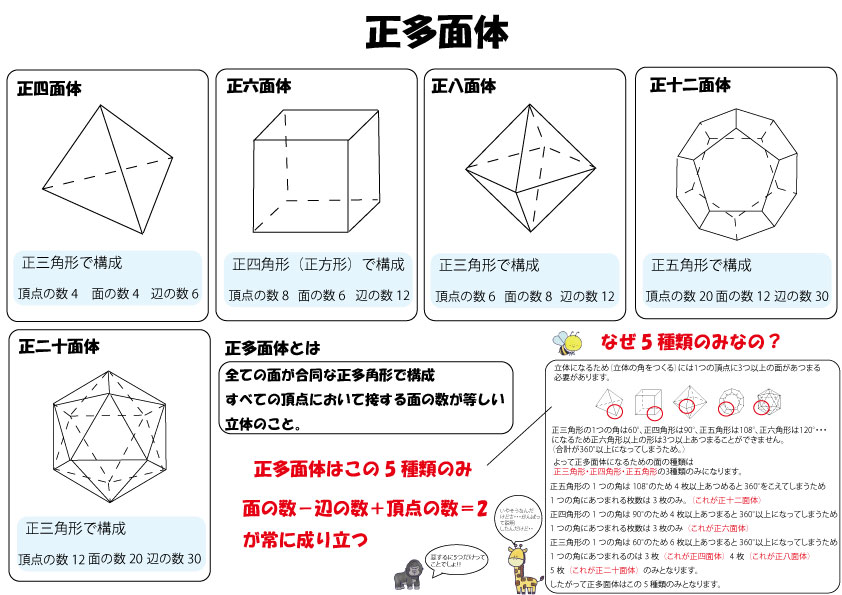
正多面体とは・・・
全ての面が合同な正多角形で構成されておりすべての頂点において接する面の数が等しい立体のことをいいます。
正多面体の種類は
正四面体・正六面体・正八面体・正十二面体・正二十面体のご種類のみです。
それぞれの面の数、辺の数、頂点の数も覚えておきましょう。
面の数、辺の数、頂点の数の間には
面の数-辺の数+頂点の数=2
という式が成り立ちます。(オイラーの多面体定理)
では正多面体はなぜ5種類のみなのでしょうか?
その理由については中学数学では習いませんが、高校数学にて学びます。
以下正多面体が5種類しかない理由です。
まず立体になるため(立体の角をつくる)には1つの頂点に3つ以上の面があつまる必要があります。
正三角形の1つの角は60°、正四角形は90°、正五角形は108°、正六角形は120°・・・
になるため正六角形以上の形は3つ以上あつまることができません。(合計が360°以上になってしまうため。)
よって正多面体になるための面の種類は正三角形・正四角形・正五角形の3種類のみになります。
正五角形の1 つの角は108°のため4 枚以上あつめると360°をこえてしまうため
1 つの角にあつまれる枚数は3 枚のみ。
(これが正十二面体)
正四角形の1 つの角は90°のため4 枚以上あつまると360°以上になってしまうため
1 つの角にあつまれる枚数は3 枚のみ
(これが正六面体)
正三角形の1 つの角は60°のため6 枚以上あつまると360°以上になってしまうため
1 つの角にあつまれるのは
3 枚(これが正四面体)
4 枚(これが正八面体)
5 枚(これが正二十面体)のみとなります。
したがって正多面体はこの5 種類のみとなります。