いろいろな相似の証明をまとめました。
解答は以下になります。
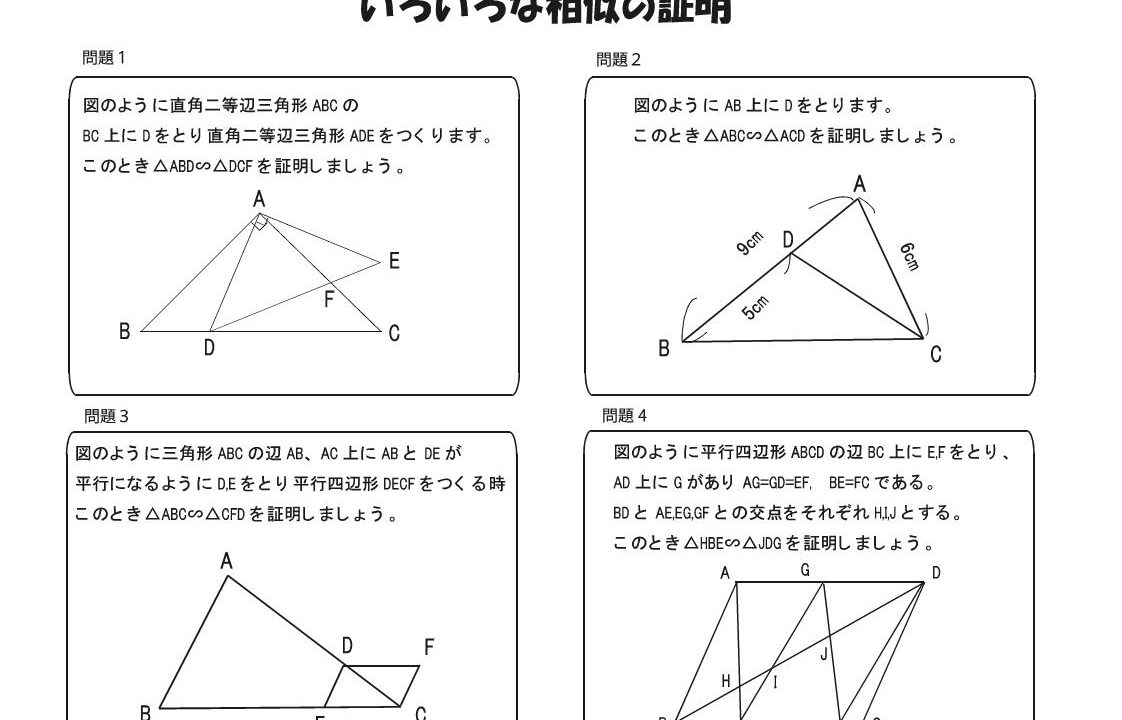
問題1
△ABDと△DCFにおいて
∠ABD=∠DCF・・・①△ABCは直角二等辺三角形より
△ABDの内角と外角の性質より
∠BAD=∠ADC-∠ABD
より
∠BAD=∠ADC-45°・・・②
また
∠CDF=∠ADC-∠ADF
より
∠CDF=∠ADC-45°・・・③
②、③より
∠BAD=∠CDF・・・④
①、④より2組の角がそれぞれ等しいので
△ABD∽△DCFとなる。
問題2
△ABCと△ACDにおいて
∠BAC=∠CAD・・・①共通な角
AB:AC=9:6=3:2・・・②
AC:AD=6:4=3:2・・・③
①②③より2組の辺の比とその間の角がそれぞれ等しいので
△ABC∽△ACDとなる
問題3
△ABCと△CFDにおいて
AB平行DE
DE平行FCより
AB平行FCなので
∠BAC=∠FCD・・・①平行線の錯角
∠CFD=∠DEC・・・②平行四辺形の対角は等しいので。
∠DEC=∠ABC・・・③平行線の同位角
②③より∠ABC=∠CFD・・・④
①④より2組の角がそれぞれ等しいので
△ABC∽△CFDとなる。
問題4
△HBEと△JDGにおいて
∠HBE=∠JGD・・・①平行線の錯角
∠DGJ=∠GFE・・・②平行線の錯角
四角形AEFGにおいて
AG=EF・・・③仮定より
AG平行EF・・・④ABCDは平行四辺形より
③④より1組の辺が平行で等しいので四角形AEFGは平行四辺形となる。
よってAE平行GFとなるので
∠BEH=∠GFE・・・⑤
∠GFE=∠DGJ・・・⑥平行線の錯角
よって
∠BEH=∠DGJ・・・⑦
①⑦より2組の角がそれぞれ等しいので
△HBE∽△JDGとなる。